附着反力-矩阵求解

附着处的合反力由几部分构成，第一个是悬臂以上结构的不平衡弯矩M产生的附着反力，第二个是悬臂以上结构所受的风载水平力，第三个是两层附着之间部分塔身所受风载的一半。

将多层附着塔身模型简化为刚性支座的连续梁，由于底部固定，因此附着几道，就是几次超静定结构。

本文只计算不平衡弯矩M产生的附着反力。

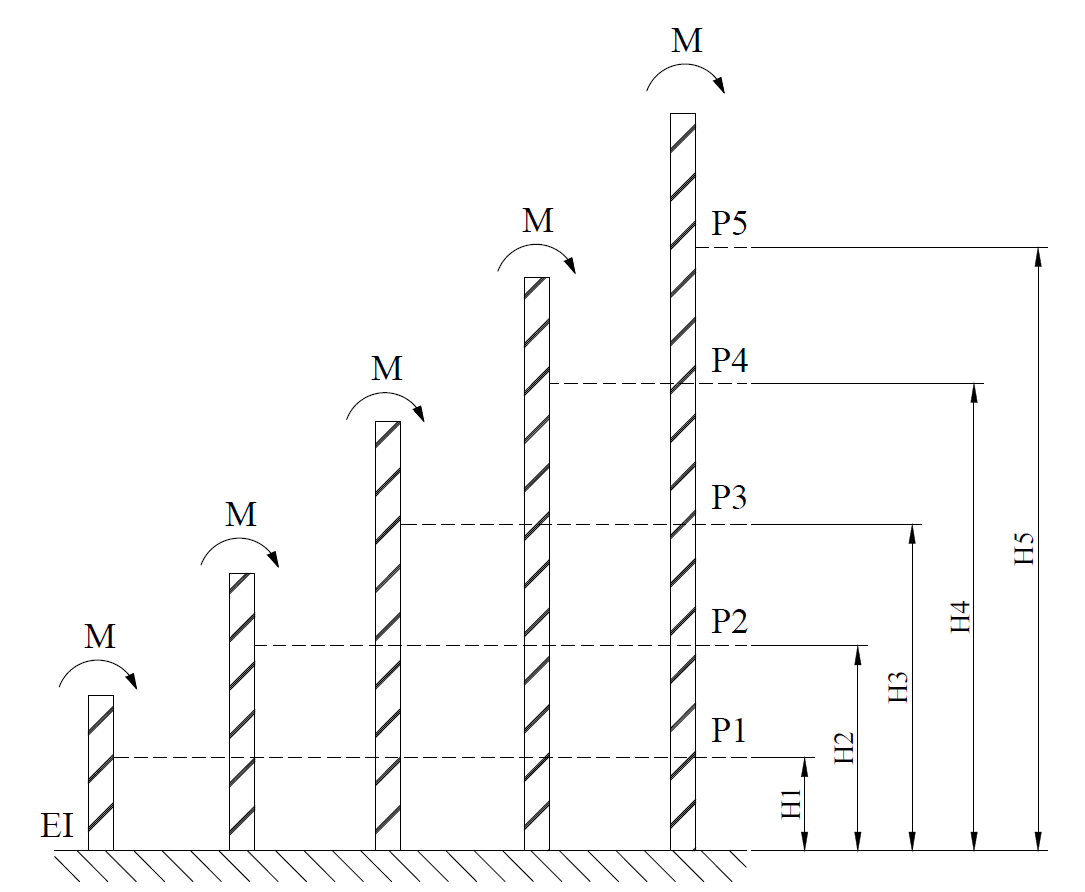
刚性支座的连续梁模型

仅有一道附着的情况

$$\frac{H_{1}^{3}}{3EI}P_1 = \frac{MH_{1}^{2}}{2EI}$$

$M$ $t·m$
$H_1$ m

有两道附着的情况

$$ \begin{bmatrix} \frac{H_{1}^{3}}{3EI} & \frac{H_{1}^{2}(3H_2-H_1)}{6EI} \\\\ \frac{H_{1}^{2}(3H_2-H_1)}{6EI} & \frac{H_{2}^{3}}{3EI} \\\\ \end{bmatrix} \begin{bmatrix} P_1 \\\\ P_2 \\\\ \end{bmatrix} = \begin{bmatrix} \frac{MH_{1}^{2}}{2EI} \\\\ \frac{MH_{2}^{2}}{2EI} \\\\ \end{bmatrix} $$

$M$ $t·m$
$H_1$ m
$H_2$ m

有三道附着的情况

$$ \begin{bmatrix} \frac{H_{1}^{3}}{3EI} & \frac{H_{1}^{2}(3H_2-H_1)}{6EI} & \frac{H_{1}^{2}(3H_3-H_1)}{6EI} \\\\ \frac{H_{1}^{2}(3H_2-H_1)}{6EI} & \frac{H_{2}^{3}}{3EI} & \frac{H_{2}^{2}(3H_3-H_2)}{6EI} \\\\ \frac{H_{1}^{2}(3H_3-H_1)}{6EI} & \frac{H_{2}^{2}(3H_3-H_2)}{6EI} & \frac{H_{3}^{3}}{3EI} \\\\ \end{bmatrix} \begin{bmatrix} P_1 \\\\ P_2 \\\\ P_3 \\\\ \end{bmatrix} = \begin{bmatrix} \frac{MH_{1}^{2}}{2EI} \\\\ \frac{MH_{2}^{2}}{2EI} \\\\ \frac{MH_{3}^{2}}{2EI} \\\\ \end{bmatrix} $$

$M$ $t·m$
$H_1$ m
$H_2$ m
$H_3$ m

有四道附着的情况

$$ \begin{bmatrix} \frac{H_{1}^{3}}{3EI} & \frac{H_{1}^{2}(3H_2-H_1)}{6EI} & \frac{H_{1}^{2}(3H_3-H_1)}{6EI} & \frac{H_{1}^{2}(3H_4-H_1)}{6EI} \\\\ \frac{H_{1}^{2}(3H_2-H_1)}{6EI} & \frac{H_{2}^{3}}{3EI} & \frac{H_{2}^{2}(3H_3-H_2)}{6EI} & \frac{H_{2}^{2}(3H_4-H_2)}{6EI} \\\\ \frac{H_{1}^{2}(3H_3-H_1)}{6EI} & \frac{H_{2}^{2}(3H_3-H_2)}{6EI} & \frac{H_{3}^{3}}{3EI} & \frac{H_{3}^{2}(3H_4-H_3)}{6EI} \\\\ \frac{H_{1}^{2}(3H_4-H_1)}{6EI} & \frac{H_{2}^{2}(3H_4-H_2)}{6EI} & \frac{H_{3}^{2}(3H_4-H_3)}{6EI} & \frac{H_{4}^{3}}{3EI} \\\\ \end{bmatrix} \begin{bmatrix} P_1 \\\\ P_2 \\\\ P_3 \\\\ P_4 \\\\ \end{bmatrix} = \begin{bmatrix} \frac{MH_{1}^{2}}{2EI} \\\\ \frac{MH_{2}^{2}}{2EI} \\\\ \frac{MH_{3}^{2}}{2EI} \\\\ \frac{MH_{4}^{2}}{2EI} \\\\ \end{bmatrix} $$

$M$ $t·m$
$H_1$ m
$H_2$ m
$H_3$ m
$H_4$ m

有五道附着的情况

$$ \begin{bmatrix} \frac{H_{1}^{3}}{3EI} & \frac{H_{1}^{2}(3H_2-H_1)}{6EI} & \frac{H_{1}^{2}(3H_3-H_1)}{6EI} & \frac{H_{1}^{2}(3H_4-H_1)}{6EI} & \frac{H_{1}^{2}(3H_5-H_1)}{6EI} \\\\ \frac{H_{1}^{2}(3H_2-H_1)}{6EI} & \frac{H_{2}^{3}}{3EI} & \frac{H_{2}^{2}(3H_3-H_2)}{6EI} & \frac{H_{2}^{2}(3H_4-H_2)}{6EI} & \frac{H_{2}^{2}(3H_5-H_2)}{6EI} \\\\ \frac{H_{1}^{2}(3H_3-H_1)}{6EI} & \frac{H_{2}^{2}(3H_3-H_2)}{6EI} & \frac{H_{3}^{3}}{3EI} & \frac{H_{3}^{2}(3H_4-H_3)}{6EI} & \frac{H_{3}^{2}(3H_5-H_3)}{6EI} \\\\ \frac{H_{1}^{2}(3H_4-H_1)}{6EI} & \frac{H_{2}^{2}(3H_4-H_2)}{6EI} & \frac{H_{3}^{2}(3H_4-H_3)}{6EI} & \frac{H_{4}^{3}}{3EI} & \frac{H_{4}^{2}(3H_5-H_3)}{6EI} \\\\ \frac{H_{1}^{2}(3H_5-H_1)}{6EI} & \frac{H_{2}^{2}(3H_5-H_2)}{6EI} & \frac{H_{3}^{2}(3H_5-H_3)}{6EI} & \frac{H_{4}^{2}(3H_5-H_3)}{6EI} & \frac{H_{5}^{3}}{3EI} \\\\ \end{bmatrix} \begin{bmatrix} P_1 \\\\ P_2 \\\\ P_3 \\\\ P_4 \\\\ P_5 \\\\ \end{bmatrix} = \begin{bmatrix} \frac{MH_{1}^{2}}{2EI} \\\\ \frac{MH_{2}^{2}}{2EI} \\\\ \frac{MH_{3}^{2}}{2EI} \\\\ \frac{MH_{4}^{2}}{2EI} \\\\ \frac{MH_{5}^{2}}{2EI} \\\\ \end{bmatrix} $$

$M$ $t·m$
$H_1$ m
$H_2$ m
$H_3$ m
$H_4$ m
$H_5$ m